Cosine Similarity Metric에 대해서
왜 알아보게 되었나?
간단하게 추천시스템을 만들때 필요한 개념들에 대해서 알아보다가 코사인 유사성 메트릭스라는 개념을 알게 되었는데, 이 개념이 유사도 추천 알고리즘에 효과적이라는 것을 알게되었다.
어떤 개념이길래 유사도 추천 알고리즘에 효과적일까? 의문이 들어서 알아보게 되었다.
코사인 유사성 메트릭스의 개념
코사인 유사성이란 쉽게 말하면, 두 데이터(벡터)가 얼마나 비슷한 방향을 가리키는지를 측정하는 방법이다.
즉, 두 데이터가 동일하거나 비슷한 속성을 많이 가질수록 유사도가 높게 나타나며 서로 다른 속성을 가질수록 유사도는 낮게 측정되는 것이다.
예를들어, 책 A와 B가 있을때 과학장르와 소설장르로 구분한다고 해보자.
이때, A책은 소설이고 B책은 과학책 일때 두 책은 서로 완전히 다른 장르를 포함하고 있어 유사도가 0으로 나타난다.
두 데이터(벡터) 사이의 각도(=세타)가 90도라면 유사도는 0이고, 0도라면 유사도는 1이 된다.
유사도는 0~1 사이에 값으로 나타낸다.
코사인 유사성의 공식은 다음과 같다.
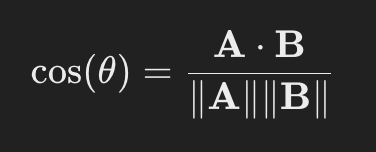
그럼 A책의 장르가 소설과 과학이 섞여있다면?
두 벡터 사이의 각도 세타가 45도일 경우 코사인 유사성 공식을 이용하여 계산하면 약 0.7이 된다. 즉, 세타가 90도에 가까우면 코사인 유사성은 0에 가깝고, 세타가 0도에 가까우면 유사성은 1에 가깝다.

코사인 45도를 계산하는 과정은 아래와 같다.


그럼 다차원 장르일 경우에는?
과학 장르와 소설 장르로 표현한 2차원에서 표현한 것처럼 다차원도 동일하게 적용된다.
두 개의 책을 다양한 장르로 나누어 벡터화하고 유사도를 계산하면 된다.

어디에 활용될 수 있나?
콘텐츠 기반 필터링 방식에서 유용하게 사용된다.
영화 장르 뿐만 아니라 줄거리 분석한 데이터를 벡터화하거나 감독, 배우 정보를 벡터화해서 콘텐츠를 추천할수도 있다. 다차원 데이터를 사용할 때는 여러 특성을 동시에 고려할 수 있어 추천의 정확도가 향상될 수 있다.
필수적인 수학개념
피타고라스의 정리 (Pythagorean Theorem)
피타고라스의 정리는 직각 삼각형에서 성립하는 수학적 법칙으로, 직각을 낀 두 변의 길이를 각각 제곱한 합은 빗변의 길이를 제곱한 것과 같다.

Sine (사인)
직각삼각형에서 한 각의 대변과 빗변의 비율을 나타낸다.
- 대변(opposite): 세타의 맞은편 변
- 빗변(hypotenuse): 삼각형의 가장 긴 변
Cosin (코사인)
직각삼각형에서 한 각의 인접변과 빗변의 비율을 나타낸다.
- 인접변(adjacent): 세타와 인접한 변
- 빗변(hypotenuse): 삼각형의 가장 긴 변

결론
코사인 유사성 메트릭스는 추천 시스템의 도구로, 콘텐츠 기반 필터링에서 유사도 계산을 통해 사용자에게 적절한 항목을 추천할 수 있다.
이를 확장하여 메타데이터, 리뷰 분석, 하이브리드 접근법을 결합하면 더욱 정교한 추천 시스템을 구축할 수 있다.